Collocation-based Robust Variational Physics Informed Neural Networks

Maciej Paszynski

Professor, AGH University of Krakow, Poland

Le 02 septembre 2025 à 13h30, Maurice Touratier room

---

Abstract: 

Since the introduction of the Physics Informed Neural Networks (PINN) [1], Artificial Intelligence can succesfully solve Partial Differential equations without using Finite Element or Finite Different solvers. We introduce a Collocation-based Robust Variational Physics-Informed Neural Networks (CRVPINNs) [2] to approximate the Partial Differential Equations (PDEs) solution, as an efficient extension of our Robust Variatonal PINNs [3]. Standard Physics Informed Neural Networks (PINN) takes into account the governing physical laws described by PDE during the learning process. The network is trained on a data set that consists of randomly selected points in the physical domain and its boundary. 

PINNs have been successfully applied to solve various problems described by PDEs with boundary conditions. The loss function in traditional PINNs is based on the strong residuals of the PDEs. This loss function in PINNs is generally not robust with respect to the true error. The loss function in PINNs can be far from the true error, which makes the training process more difficult. In particular, we do not know if the training process has already converged to the solution with the required accuracy. This is especially true if we do not know the exact solution, so we cannot estimate the true error during the training. The Variational PINN is an extension of PINNs where the strong residuals are replaced by the weak residuals [4]. The loss function of VPINN is also not robust [3].

This talk introduces a different way of defining the loss function.

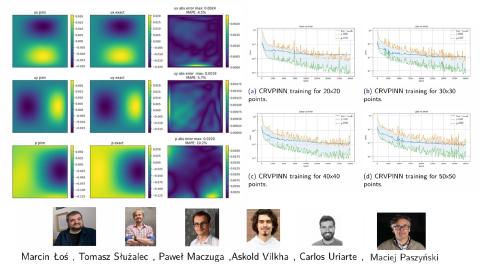
We redefine the loss function from VPINN to create a Robust Variational PINN method. Our loss incorporates the residual and the inverse of the Gram matrix, computed using the energy norm.

Additionally, we introduce the collocation method to speedup the RVPINN solver. We test our CRVPINN algorithm on Laplace problems, advection-diffusion problems, and Stokes problems. We conclude that our Collocation-based RVPINN is a robust method. The proposed loss is related with the true error of the solution, as measured in the energy norm. Thus, we know if our training process goes well, and we know when to stop the training to obtain the neural network approximation of the solution of the PDE with the true error of required accuracy. Our numerical examples rely on the Python Google Colab library [5] that we recently developed. We also discuss the efficiency of the method and compare it to Finite Element and Finite Difference solvers.

 

[1] George Em Karniadakis, Ioannis G. Kevrekidis, Lu Lu, Paris Perdikaris, Sifan Wang, Liu Yang, Physics-informed machine learning, Nature Reviews Physics 3 (2021) 422–440

[2] Marcin Łoś, Tomasz Służalec, Paweł Maczuga, Askold Vilkha, Carlos Uriarte, Maciej Paszyński, Collocation-based Robust Variational Physics-Informed Neural Networks (CRVPINN) (2024)

[3] Sergio Rojas, Paweł Maczuga, Judit Muñoz-Matute, David Pardo, Maciej Paszynski, Robust Variational Physics-Informed Neural Networks, Computer Methods in Applied Mechanics and Engineering (2024)

[4] Ehsan Kharazmi, Zhongqiang Zhang, George E.M. Karniadakis, hp-VPINNs: Variational physics-informed neural networks with domain decomposition, Computer Methods in Applied Mechanics and Engineering (2021)

[5] Paweł Maczuga, Maciej Sikora, Maciej Skoczeń, Przemysław Rożnawski, Filip Tłuszcz, Marcin Szubert, Marcin Łoś, Witold Dzwinel, Keshav Pingali, Maciej Paszyński, Physics Informed Neural Network Code for 2D Transient Problems (PINN-2DT) Compatible with Google Colab. In: Lees, M.H., et al. Computational Science – ICCS 2025. ICCS 2025. Lecture Notes in Computer Science, vol 15904. Springer, Cham. 

Biography: 

Maciej Paszyński is a Full Professor of Computer Science at AGH University of Krakow, Poland. He received his PhD in Mathematics with Applications to Computer Science from Jagiellonian University (2003) and has since authored over 230 Scopus-indexed publications. His research focuses on artificial intelligence, adaptive algorithms, and high-performance computing for advanced simulations. He collaborates with international research centers, including the Oden Institute at the University of Texas at Austin, and leads the Adaptive Algorithms and Systems group at AGH. He is the Workshops on Computational Science Chair in the frame of the International Conference on Computational Science. He has supervised 10 PhD students with distinction and is the AGH leader of EU project IN-DEEP.